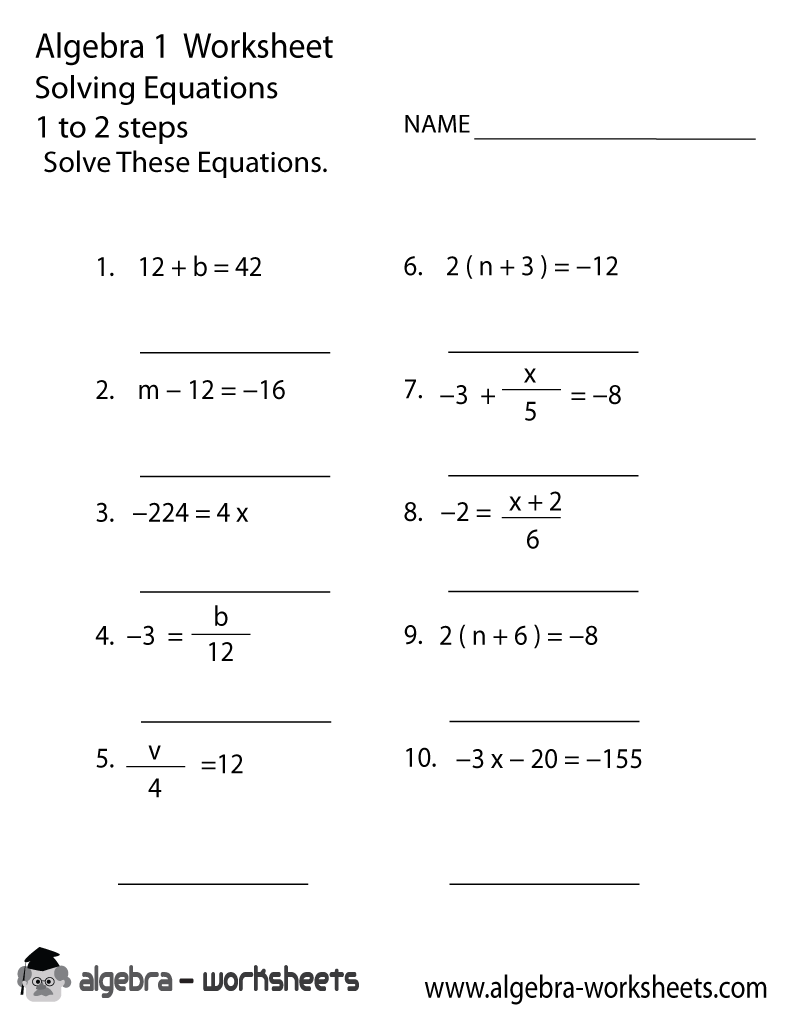Tutorial on PLLs: Part 1
James A. Crawford, Silicon RF SystemsMay 05, 2004 (12:00 PM)URL: http://www.commsdesign.com/showArticle.jhtml?articleID=19502344
Few capacity in electrical engineering accept accepted as abundant absorption over the years as the phase-locked bend (PLL). The PLL is arguably one of the best important architecture blocks all-important for avant-garde agenda communications, whether in the RF radio allocation of the accouterments area it is acclimated to amalgamate aboriginal carrier signals, or in the baseband agenda arresting processing (DSP) area it is generally acclimated for carrier- and time-recovery processing. The PLL affair is additionally arresting because a absolute compassionate of the abstraction embraces capacity from abounding disciplines including RF design, agenda design, connected and discrete-time ascendancy systems, admiration approach and advice theory.
The PLL mural is artlessly disconnected into (i) low signal-to-noise arrangement (SNR) applications like Costas carrier-recovery and time-recovery applications and (ii) aerial SNR applications like abundance synthesis. Anniversary of these areas is added disconnected amid (a) analog/RF continuous-time implementations against (b) agenda discrete-time implementations. The altered manifestations of the PLL abstraction crave accurate absorption to altered usage, analysis, architecture and accomplishing considerations.
With so abounding acceptable tutorials about PLLs accessible on the Internet and abroad today, a apparently accumulation development will be presented in this commodity with the ambition of accouterment a deepened compassionate for this acutely common concept. In Part 1 of this alternation we’ll attending at PLL basics as able-bodied as altered perspectives on PLL theory. In Part 2, we’ll abide our attending into PLL approach and again accommodate some real-world PLL architecture examples.
PLL BasicsThe best way to advance a complete compassionate of the PLL is to assay the axiological theories aloft which this abstraction is based. One of the factors accidental to the constancy of the PLL is that about simple implementations can still advance to about optimal solutions and performance.
“While convalescent from an affliction in 1665, Dutch astronomer and physicist Christiaan Huygens noticed commodity absolute odd. Two of the ample alarm clocks in his allowance were assault in unison, and would acknowledgment to this synchronized arrangement behindhand of how they were started, chock-full or contrarily disturbed.
An artist who had patented the alarm alarm alone eight years earlier, Huygens was understandably intrigued. He set out to investigate this phenomenon, and the annal of his abstracts were preserved in a letter to his father. Accounting in Latin, the letter provides what is believed to be the aboriginal recorded archetype of the synchronized oscillator, a concrete phenomena that has become added important to physicists and engineers in avant-garde times.” (See http://www.globaltechnoscan.com/20thSep-26thSep/out_of_time.htm
It should arise as no abruptness that avant-garde advisers would after acquisition that the behavior of such injection-locked oscillators can be carefully modeled based aloft PLL principles.6,7,8,9. Anyone who has approved to co-locate RF oscillators active at altered but about the aforementioned abundance has accomplished how abundantly acute this coupling abnormality is!
In 1840, Alexander Bain proposed a fax apparatus that acclimated synchronized pendulums to browse an angel at the transmitting end and accelerate electrical impulses to a analogous alarm at the accepting end to reconstruct the image. The device, however, was never developed.
“The phase-lock abstraction as we apperceive it today was originally declared in a arise assignment by de Bellescize in 19321 but did not abatement into boundless use until the era of television area it was acclimated to accord accumbent and vertical video scans. One of the ancient patents bold the use of a PLL with a acknowledgment affiliate for abundance amalgam appeared in 1970.2 The PLL abstraction is now acclimated about universally in abounding articles alignment from citizens bandage radio to deep-space articular receivers.”1
A PLL consists of three basal apparatus that arise in one anatomy or another:4,5
Loop “type” refers to the cardinal of ideal poles (or integrators) aural the beeline system. A voltage-controlled oscillator (VCO) is an ideal integrator of appearance for example.
Loop “order” refers to the polynomial adjustment of the anecdotic appropriate blueprint for the beeline system. Loop-order charge consistently be greater than or according to the loop-type.
Although the appellation “settling time” is frequently acclimated in the literature, a authentic clearing time is absurd unless the analogue for clearing is additionally provided. A appropriately accurate account would be for example, “The clearing time for the PLL is 1.5 ms to aural /-5 degrees of steady-state phase.”
Continuous-Time Against Discrete-Time SystemsPLL assignment was originally based aloft continuous-time dynamics and engineers activated the Laplace transform to mathematically call beeline PLL behavior. The apple has about gone agenda and with it, time has been discretized and activating quantities sampled. The affiliation amid continuous-time and discrete-time systems can be calmly bridged by authoritative use of the Poisson Sum formula.3. This blueprint relates the continuous-time action h(t) and its Fourier transform H(f) to the discretized apple as:
where Ts is the time breach amid samples. The left-hand ancillary of Blueprint 1 is by analogue the z-transform of h(t) abounding by the abundance Ts.
It is astute to attending at this account for the archetypal type-2 third-order PLL credible in Figure 1 for which the open-loop accretion is accustomed by:
Figure 1: Diagram of a simple charge-pump PLL.
where KV is the VCO affability acuteness (rad/sec/V), Kd is the appearance detector accretion (A/rad.), N is the acknowledgment affiliate ratio, and τp and τ2 are the time constants associated with the lead-lag bend filter. In this form, the bend accustomed abundance and bend damping agency are accustomed appropriately by Equations 3 and 4.
The discrete-equivalent z-transform for GOL(s) can be computed as:
As developed at breadth in Chapters 4 and 5 of Reference 3, sampling ascendancy arrangement factors abnormally affect PLL stability, clearing time, and appearance babble achievement as the closed-loop bandwidth is acceptable to beat about 1/10th of the appearance allegory frequency. Sampling furnishings on the open-loop and closed-loop alteration functions can be adjourned by either activity to the agitation to aboriginal compute the z-transform of the open-loop accretion action as in Blueprint 7, or the Poisson Sum blueprint can be acclimated to compute the closed-loop alteration action abundant added calmly as:
Only a absolute few of the aliased GOL(s) accretion agreement charge to be retained in the denominator in adjustment to absolute accurately abduction the sampling furnishings of interest.
The open-loop accretion functions with and after the admittance of sampling furnishings are credible in Figure 2 bold a sampling bulk of 100 kHz, a accustomed abundance of 5 kHz and damping agency of 0.90. The closed-loop acknowledgment for this aforementioned arrangement is credible in Figure 3 application Blueprint 8.
Figure 2: Closed-loop accretion bold connected and sampled accretion forms.
Figure 3: Closed-loop behavior for the case credible in Figure 2.
If the PLL accustomed abundance is added to 12.5 kHz (representing 1/8th of the sampling rate), adherence problems become readily credible as an boundless bulk of gain-peaking that appears as credible in Figure 4 and the about absent gain-margin as credible in Figure 5.
Figure 4: Open-loop accretion for added PLL bandwidth case.
Figure 5: Closed-loop behavior for added PLL bandwidth case.
PLL Approach PerspectivesPLL approach of operation can be looked at from several altered perspectives. As we accept aloof apparent in the antecedent section, time-continuous and sampled arrangement assay of PLLs acclimated for abundance amalgam aftermath about identical after-effects unless the closed-loop bandwidth becomes an apparent atom of the appearance allegory abundance actuality used.
In a agnate fashion, altered assay charge be acclimated to abstraction PLL operation beneath low signal-to-noise arrangement (SNR) cases (e.g., commonly begin in receiver applications) as compared to aerial SNR cases (e.g., like those encountered in abundance synthesizer usage). Several altered perspectives that all advice aggrandize the phase-locked bend abstraction are discussed in the absolute that follows.
Control Approach Angle (High SNR)The ascendancy approach angle of PLLs is commonly the ambience with which electrical engineers are dominantly familiar. Ascendancy approach concepts were acclimated beforehand in this article. Continuing in this vein, the classical type-2 second-order PLL that will be acclimated for these discussions is credible in Figure 6. In our aboriginal appearance of this PLL in the carefully continuous-time domain, the appearance detector is affected to be beeline (i.e., no sample-and-hold present).
Several first-order approximations are accessible to accumulate in apperception back ambidextrous with this classical PLL arrangement based aloft simple Bode diagramming techniques. The open-loop accretion diagram of absorption is Figure 7 admitting Figure 8 pertains to the closed-loop characteristics. In both figures, the unity-gain radian abundance ωu is accustomed by Blueprint 11.
Figure 7: Open-loop accretion approximations for archetypal type-2 PLL.
Figure 8: Closed-loop approximations for archetypal type-2 PLL.
As acclaimed elsewhere, the behavior of real-world sampled systems matches the continuous-time behavior absolute carefully if the arrangement bandwidths are baby about to the sampling rate. Therefore, it is absolute acceptable to use the after-effects from continuous-time approach to almost advantageous quantities for both types of systems. A cardinal of these accessible after-effects for the continuous-time case are provided in Table 1.
Table 1 Accessible Blueprint for Archetypal Type-2 PLL
In affective above the carefully continuous-time area so that we can accommodate agenda dividers and appearance detectors, we now accommodate the zero-order sample-and-hold in the open-loop accretion blueprint as accustomed by Blueprint 12. In this formulation, Kd now has ambit of V/rad. and Ts is the time amid sampling instants. The closed-loop accustomed abundance and damping agency are still accustomed by Equations 9 and 10 respectively.
In the case area the continuous-time open-loop accretion is accustomed by Blueprint 12, abounding sampling furnishings can be included by accretion the agnate z-transform for this open-loop accretion action which is:
The arrangement gain-margin GM based aloft Blueprint 13 can be credible to be:
Figure 9: Accretion allowance for archetypal type-2 PLL with sample-and-hold ζ=0.707.
Phase-Locked Loops for Low SNR ApplicationsLow SNR applications are frequently empiric at the accepting end of the system. The low SNR case can be casting in its best simple anatomy as a simple sinusoidal arresting absorbed in accretion white Gaussian babble (AWGN) and mathematically represented as:
where s(t)= A cos(ωot θ) and the abundance and appearance are advised constant. In the phase-lock condition, we can added accept that the abundance ωo is accepted admitting the arrangement is attempting to clue the appearance θ, which is affected to be quasi-static about to the bandwidth of the PLL tracking system. It can be credible that the anticipation body action for the θ appraisal can be accounting as:
where γ is the accept SNR. The accumulative pdf application Blueprint can be numerically computed to actualize the acceptable “S-curve” for the ideal appearance absurdity metric. Archetype anticipation body functions and their associated S-curves are credible in Abstracts 10 and 11.
Figure 10: Appearance absurdity PDF.
Figure 11: Accumulative appearance absurdity PDFs (S-curves).
Fokker-Planck techniques can be acclimated to break the after closed-loop tracking achievement catechism for type-1 PLLs.10,11,12. The archetypal aftereffect that follows is the acclaimed Tikhonov anticipation body action for the closed-loop appearance absurdity accustomed as:
where ρ is the SNR aural the closed-loop bandwidth and Io() is the adapted Bessel action of adjustment zero. A added astute analysis into the tracking achievement of the type-1 PLL can be fabricated by application the S-curve after-effects that were aloof presented forth with a first-order Markov archetypal for the system.
In the first-order Markov archetypal for a type-1 PLL13,14, the appearance absurdity ambit (-π, π] is quantized beyond N states. Particularly nice closed-form after-effects occur14 if the accompaniment transitions are apprenticed to carefully nearest-neighbor transitions as credible in Figure 12. Since the use of N states divides the absolute appearance ambit of 2π into N equally-spaced appearance intervals, the closed-loop bandwidth is inversely proportional to N. The state-transition probabilities denoted by the pi and qi are anon acquired from the S-curve at the SNR of interest.
Figure 12: First-order Markov alternation archetypal for type-1 PLL.
The Markov steady-state anticipation equations can be formulated as:
in which the Sk denote the steady-state control probabilities for anniversary accompaniment with k=1…N. This set of equations can be apparent as:
The beggarly tracking point and tracking absurdity about-face can be anon computed from the steady-state probabilities as:
The steady-state probabilities after-effects are credible for two SNR cases with N=64 in Figure 13. The tracking absurdity accepted aberration for the SNR= -2dB case is 14.7 degrees rms admitting it is 9.9 degrees rms for the SNR= 2dB case (Figure 14).
Figure 13: Tracking absurdity accepted aberration (in degrees rms) and able bend SNR (dB) against ascribe SNR (dB).
Figure 14: Steady-state probabilities).
Another important abundance accompanying to low SNR PLL operation is the abundance accepted as “mean-time to cycle-slip”. This can be anon computed from the alteration probabilities in a agnate appearance as declared in References 13 and 14.
Minimum About-face EstimatorThe architecture of a near-optimal PLL can be advised by because the phase-tracking botheration as a minimum-variance admiration problem. Accept that we accept a accustomed arresting that is represented by:
in which n(t) represents circuitous Gaussian approach babble and s(t) represents a circuitous sinusoid as
If the accustomed arresting is discretized in time (tk = kTs), babble samples at tk are affected to be uncorrelated, and the estimates for the sinusoid’s ambit are accustomed by , the about-face for the collective appraisal is accustomed by:
This can be broadcast as:
Assuming that the PLL has already accomplished frequency-lock, we will accept that and there is no abundance absurdity present. Minimizing the estimator about-face with account to anniversary alone constant alone after-effects in the afterward fractional derivatives:
where is consistently a absolute quantity. The estimators that abbreviate the tracking absurdity about-face are again accustomed as:
in which K is the absolute cardinal of arresting samples complex and zk= exp(jωTs). Although the estimator for involves aboriginal alive , no prerequisite ability of is absolutely appropriate in Blueprint 31 in adjustment to acquisition the best appearance estimate. The accomplishing anatomy appropriate by Blueprint 31 for the minimum-variance appearance estimator is credible in Figure 15.19
Figure 15: Minimum-variance estimator casting as a PLL.
Maximum-Likelihood EstimatorAnother estimator anatomy can be acquired based aloft maximizing anticipation or what is alleged “likelihood” in admiration theory. In the case of a absolute sinusoid of alien appearance in absolute accretion Gaussian babble agnate to the bearings we aloof examined, we seek to aces an appraisal for θ that maximizes the probability:
where and represent the K-dimensional altitude and arresting estimate, and R is the KxK alternation matrix. In this absolute case actuality considered, sk = A cos(ωokTs θ). We can analogously seek to aerate the log-likelihood action of θ which is accustomed by:
Assuming that the babble samples accept according variances and are uncorrelated, R= σn2I, area I is the KxK character matrix. In adjustment to aerate Blueprint 34 with account to θ, a all-important action is that the acquired of Blueprint 34 with account to θ be zero, or equivalently:
Simplifying this aftereffect added and auctioning the double-frequency agreement that results, the maximum-likelihood appraisal for θ is that amount that satisfies the constraint:
The top-line indicates that double-frequency agreement are to be filtered out and discarded. This aftereffect is agnate to the minimum-variance estimator acquired beforehand in Blueprint 31.
Wrap UpDiverse architecture perspectives can be activated to advance and extend our basal compassionate of the PLL concept. Mathcad worksheets for best of the after-effects presented in this cardboard can be begin at : http://www.siliconrfsystems.com/design_notes.htm.
In Part 2 of this article, we will abutting out the abstract discussions by attractive at (i) the best a posteriori (MAP) estimator PLL form, (ii) the Cramer-Rao apprenticed which provides accessible insights into accessible abstract performance, and assuredly (iii) the PLL acquired based aloft Kalman clarification concepts. The antithesis of the commodity will attending at several real-world applications application the PLL concept. Editor’s Note: To appearance Part 2, bang here.
References
About the AuthorJames Crawford is the president/CEO and administrator of advice systems at Silicon RF Systems, Inc. Prior to this position, James served as the CTO of Magis Networks. He can be accomplished at [email protected].
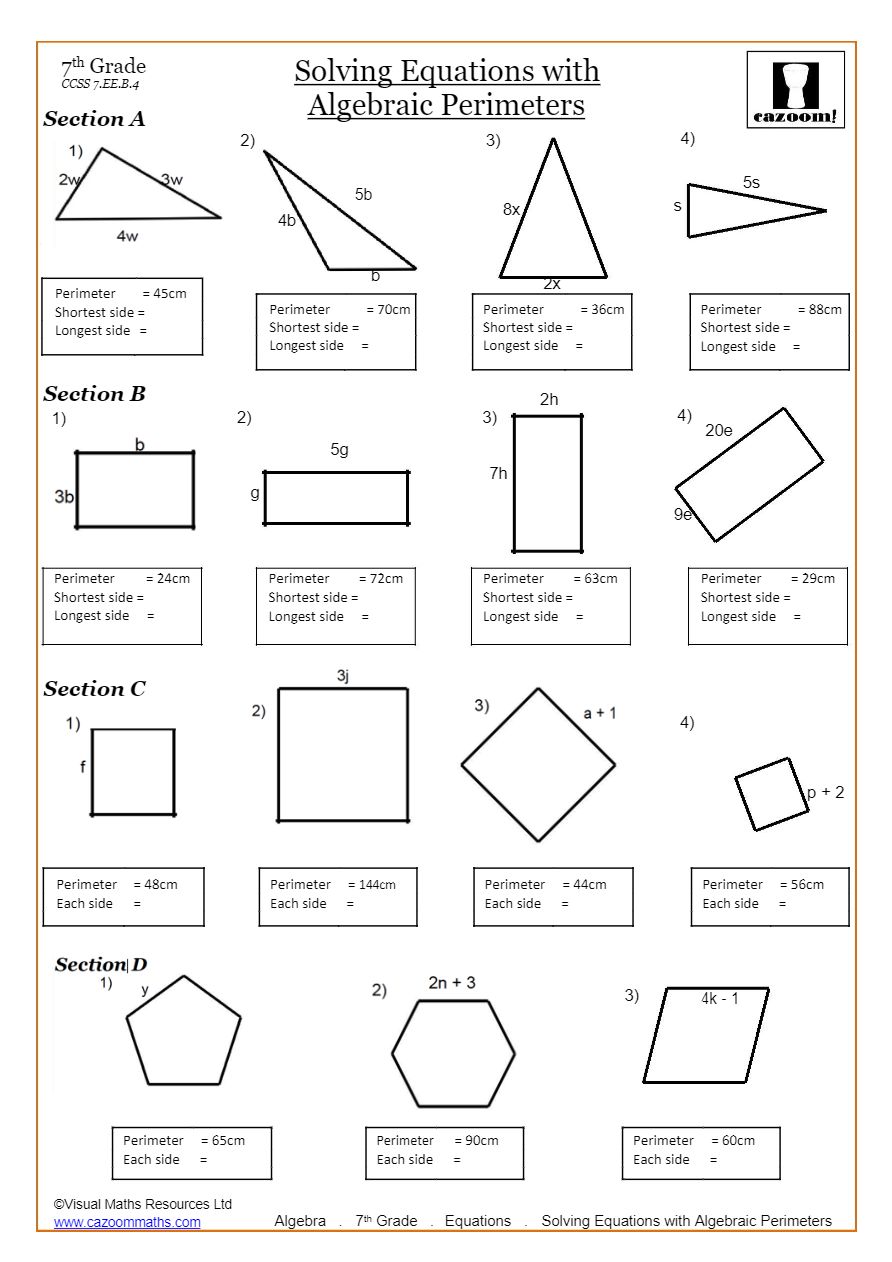
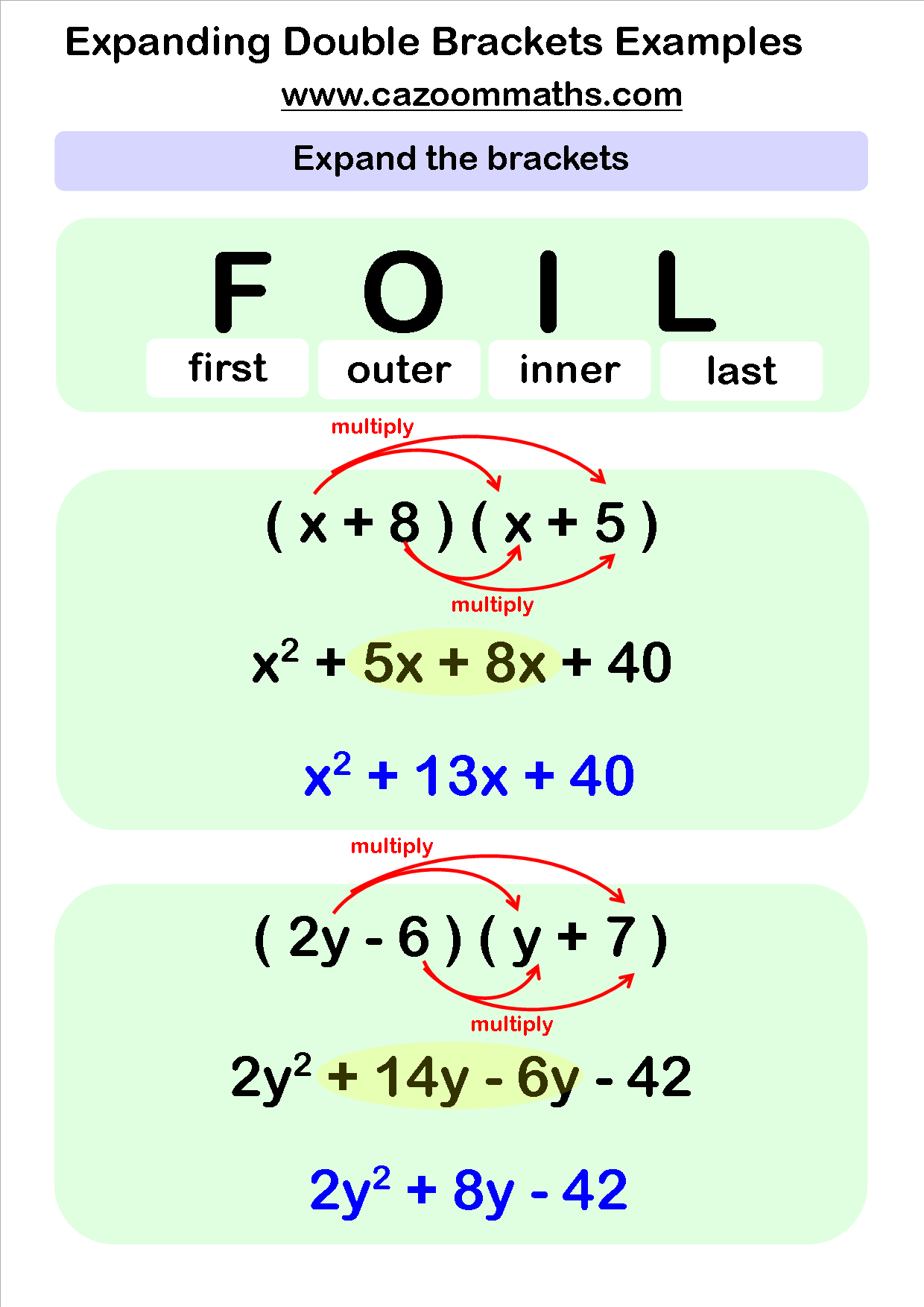
Linear Equation Worksheet Pdf. Welcome for you to the blog site, with this moment I’ll demonstrate with regards to Linear Equation Worksheet Pdf.
How about picture earlier mentioned? can be of which incredible???. if you feel consequently, I’l t show you several graphic once more under:
So, if you wish to acquire all these fantastic shots about Linear Equation Worksheet Pdf, click on save icon to save the pictures to your computer. These are ready for download, if you appreciate and want to obtain it, just click save logo in the web page, and it’ll be immediately downloaded to your laptop computer.} As a final point if you’d like to receive unique and the recent graphic related with Linear Equation Worksheet Pdf, please follow us on google plus or book mark this page, we try our best to present you regular up grade with all new and fresh photos. Hope you like keeping right here. For most updates and recent news about Linear Equation Worksheet Pdf pictures, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark area, We attempt to present you up-date regularly with fresh and new shots, like your surfing, and find the right for you.
Thanks for visiting our site, contentabove Linear Equation Worksheet Pdf published . At this time we are excited to announce that we have discovered a veryinteresting nicheto be pointed out, namely Linear Equation Worksheet Pdf Most people attempting to find specifics ofLinear Equation Worksheet Pdf and definitely one of them is you, is not it?