Rational And Irrational Numbers Worksheet. In this chapter, we’ll ensure your expertise are firmly set. Surds are non-perfect squares or cubes that can’t be simplified and take away the square or dice roots. And, yes, I’m the loopy teacher who wore a sticker around ALL DAY that learn 3/8. If you missed this drawback, evaluate Example 5.1.4.
We’ll take one other have a glance at the kinds of numbers we now have worked with in all previous chapters. We’ll work with properties of numbers that will help you improve your number sense.

One class barely made it through subtraction. This is a picture of a foldable that I created for my college students to use as they walked by way of a rational and irrational numbers exploration activity.
Difference Between Rational And Irrational Numbers
You have solved many different varieties of purposes. You have established a good solid basis that you just need so you can be successful in algebra.

The students are asked to explain each vocabulary word in their very own phrases and give an instance of each. They are given the project firstly of the unit, and turn it in at the finish of the unit.
Distinction Between Rational And Irrational Numbers
Students will learn to determine if numbers are rational or irrational. A sample problem is solved and two follow problems are offered.
What is the sq. root of 64?
The square root of 64 is eight, i.e. √sixty four = eight.
These slides will take you thru some duties for the lesson. If you have to re-play the video, click the ‘Resume Video’ icon. If you are requested to add answers to the slides, first obtain or print out the worksheet.
Classifying Rational And Irrational Numbers
You have completed the first six chapters of this book! It’s time to take stock of what you may have carried out so far in this course and think about what is ahead.

This implies that all integers, complete numbers, and pure numbers aren’t Irrational Numbers, they’re instead Rational Numbers. The most common examples of Irrational Numbers are π, √2, √3, and e. A fast reference for students learning about good squares and sq. roots.
In degree 1, college students are requested to determine whether or not a number is rational or irrational. In degree 2, college students are requested to determine whether or not the sum, distinction, product, or quotient of two numbers is rational or irrational. A worksheet/activity to help college students decide between rational and irrational Numbers Great device to check their knowledge.
Typically Irrational Numbers are numbers like pi and square roots. Rational numbers could be written as a fraction of two integers, whereas irrational numbers can’t. Help college students be taught to appropriately identify each with this eighth-grade quantity sense worksheet!
E-book Your Class Now!
Because it’s 4 instances four occasions four, 4 is an entire number which implies the dice root of sixty four is rational number. Great for introducing Rational and Irrational Numbers or as a 2nd day extension activity. Students can work in pairs for the entire activity or only part of it.

Rational Numbers are numbers that can be written as a fraction. This contains whole numbers, terminating decimals, and repeating decimals as a end result of you’ll have the ability to write them all as fractions. Irrational Numbers are numbers that can’t be written as a fraction.
Share This:
We have also seen that each fraction is a rational number. Look at the decimal form of the fractions we simply considered.

The third kind of rational numbers are repeating decimals. Most commonly you will notice level three repeating which is one-third or zero.6 repeating which might be 2/3. It’s any decimal that repeats the same pattern over and over again.

You have discovered how to add, subtract, multiply, and divide whole numbers, fractions, integers, and decimals. You have turn into familiar with the language and symbols of algebra, and have simplified and evaluated algebraic expressions.

When we put together the rational numbers and the irrational numbers, we get the set of actual numbers. Figure \(\PageIndex\) illustrates how the quantity sets are associated.
In your personal phrases, explain the distinction between a rational number and an irrational quantity. Does the term “real numbers” seem unusual to you? Are there any numbers that are not “real”, and, if so, what may they be?

•The addition or the multiplication of two irrational numbers could additionally be a rational quantity. Students reveal their proficiency identifying rational and irrational numbers. Students will decide if numbers are rational or irrational.

Sarah Carter is a high school math teacher who passionately believes that math equals love. Through this weblog, she strives to equip other teachers to create inviting and fascinating lecture rooms where studying mathematics is fun.
In truth we can’t write the square root of two utilizing a ratio of two numbers … This worksheet explains tips on how to evaluate two rational numbers.

Students learn how to establish reciprocals and inverses. Students will label numbers as rational or irrational. The square root of all sq. numbers are irrational numbers.

Because 7.3 means \(7 \dfrac\), we are able to write it as an improper fraction, \(7 \dfrac\). So 7.3 is the ratio of the integers 73 and 10. To decide if an integer is a rational number, we attempt to write it as a ratio of two integers.

For instance if we’ve the whole number of six, all complete numbers technically have this one underneath of them, as a result of it’s like saying 6 divided by one. We typically do not write this one because obviously 6 divided by one is simply six so you wouldn’t have to put in writing it because it doesn’t change the number. When you see a complete number, it doesn’t matter what the whole quantity is, there’s a divided by one or a fraction one underneath of it.

Two portions are within the golden ratio if their ratio is identical because the ratio of their sum to the bigger of the two quantities. Zero is a rational quantity as it can be computed as zero in a fraction. Zero divided by any integer will equal to a zero.
Is 2.71828 a rational number?
It is an infinite non-repeating decimal number. e is a math symbol with decimal worth 2.71828… It cannot be written as a ratio of two integers. It is an infinite non-repeating decimal number.
Now a rational quantity is any quantity that you could write as a ratio of two numbers. In other words, any quantity you could write as a fraction.

Let’s summarize a technique we can use to find out whether or not a number is rational or irrational. Given decimals, college students will categorical their values as fractions.
In this article, we discuss 7 variations between rational and irrational numbers. This worksheet evaluations rational and irrational numbers. A sample problem is solved and six follow issues are provided.

Three offers us adverse 8 which is a complete number. Now we know negative 8 can be re-written as adverse eight over 1 and unfavorable eight over 1 is a fraction, which means it’s rational number. In order to simplify this we have to find what number times what number instances what quantity equals sixty four.

You can write this as a fraction as a end result of you presumably can rewrite 1.75 as a combined quantity. It would be 1 and 75 over a hundred which might be the unsimplified version however it simply proves that you could write it as a fraction. Based on whether or not an actual number could be represented in type of p/q, we are in a position to classify numbers as rational and irrational numbers.

So, I truly went through the activity with my students. I didn’t take off my sticker because I figured I would simply need to make one other one to put on for third hour and sixth hour.
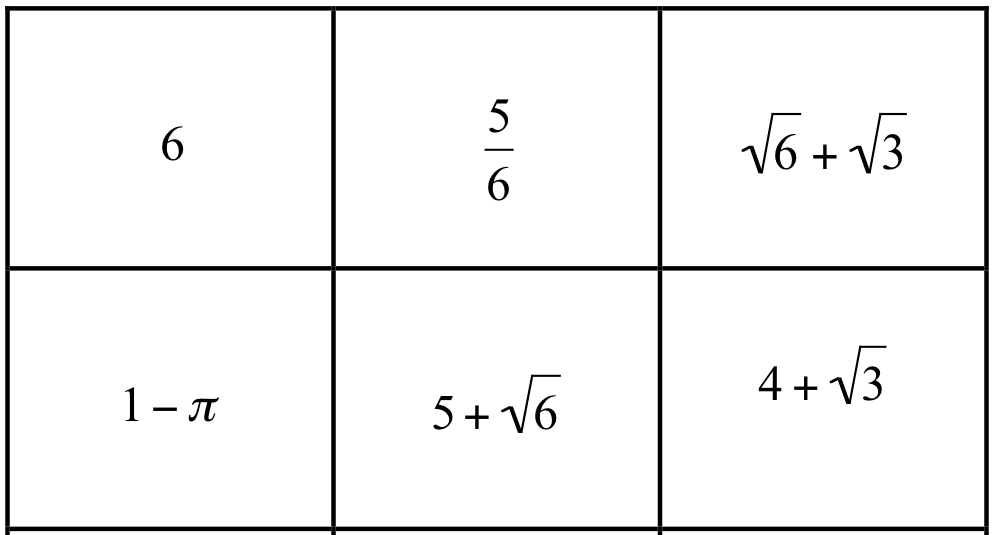
As students got here in the classroom, they got to select a random number from the pile. Apparently Hippasus (one of Pythagoras’ students) discovered irrational numbers when attempting to write down the sq. root of two as a fraction .

Great for introduction to rational and irrational numbers. Students can even create their own after sorting.

For centuries, the only numbers folks knew about have been what we now name the actual numbers. Then mathematicians found the set of imaginary numbers. You won’t encounter imaginary numbers on this course, however you will in a while in your research of algebra.

After one class period, we had solely started to scratch the surface. I ended up by no means ending this exercise with my college students as a end result of I felt a necessity to maneuver on. Rational numbers embody good squares like 9, 16, 25, 36, 49 etc.
[ssba-buttons]